Teorema del binomio
En matemática, el teorema del binomio
es una fórmula que proporciona el desarrollo de la potencia n-ésima de n
(siendo n, entero positivo) de un binomio. De acuerdo con el teorema,
es posible expandir la potencia (x + y)n en una suma que implica términos de la forma axbyc, donde los exponentes b y c son números naturales con b + c = n, y el coeficiente a de cada término es un número entero positivo que depende de n y b. Cuando un exponente es cero, la correspondiente potencia es usualmente omitida del término. Por ejemplo,
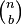 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).
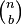 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).Formulación del teorema
Este teorema establece: Usando la fórmula para calcular el valor de (que también es representado ocasionalmente como
(que también es representado ocasionalmente como  o
o 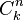 ) se obtiene la siguiente representación:
) se obtiene la siguiente representación:El coeficiente de |
 recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:
recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:Ejemplo
Como ejemplo, para n=2, n=3, n=4, utilizando los coeficientes del triángulo de Pascal:(2)Para obtener la expansión de las potencias de una resta, basta con tomar -y en lugar de y en los términos con potencias impares de y. La expresión (2) queda de la siguiente forma:
Relación de recurrencia
En matemática, una relación de recurrencia es
una ecuación que define una secuencia recursiva; cada término de la
secuencia es definido como una función de términos anteriores.
Definición
Una ecuación recurrente es un tipo específico de relación de recurrencia. Una relación de recurrencia para la sucesión es una ecuación que relaciona
es una ecuación que relaciona  con alguno de sus predecesores
con alguno de sus predecesores  . Las condiciones iniciales para la sucesión
. Las condiciones iniciales para la sucesión 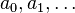 son valores dados en forma explícita para un número finito de términos de la sucesión.1
son valores dados en forma explícita para un número finito de términos de la sucesión.1Resolver una relación de recurrencia consiste en determinar una fórmula explícita (cerrada) para el término general
 , es decir una función no recursiva de n.
, es decir una función no recursiva de n.Hay dos métodos para resolver relaciones recurrentes: iteración y un método especial que se aplica a las relaciones de recurrencia lineales homogéneas con coeficientes constantes.
Un ejemplo de una relación de recurrencia es el siguiente:
Resolución
Iteración
Para resolver una relación de recurrencia asociada a la sucesión: por iteración, utilizamos la relación de recurrencia para escribir el n-ésimo término
por iteración, utilizamos la relación de recurrencia para escribir el n-ésimo término  en términos de algunos de sus predecesores. Luego utilizamos de manera
sucesiva la relación de recurrencia para reemplazar cada uno de los
términos por algunos de sus predecesores. Continuamos hasta llegar a
alguno de los casos base.
en términos de algunos de sus predecesores. Luego utilizamos de manera
sucesiva la relación de recurrencia para reemplazar cada uno de los
términos por algunos de sus predecesores. Continuamos hasta llegar a
alguno de los casos base.Recurrencias Lineales
Una relación de recurrencia es lineal de grado k si tiene la siguiente estructura: funciones reales de
funciones reales de  , y
, y  una función de n.
una función de n.El adjetivo lineal indica que cada término de la secuencia está definido como una función lineal de sus términos anteriores. El orden de una relación de recurrencia lineal es el número de términos anteriores exigidos por la definición.
En la relación
 el orden es dos, porque debe haber al menos dos términos anteriores (ya sean usados o no).
el orden es dos, porque debe haber al menos dos términos anteriores (ya sean usados o no).Ejemplos :
Ecuación de Recurrencia lineal homogénea con coeficientes constantes
Se llama ecuación de recurrencia lineal homogénea de grado k, con coeficientes constantes, a una expresión del tipo: , siendo k el grado de la ecuación.
, siendo k el grado de la ecuación.La recurrencia lineal, junto con las condiciones iniciales
 , determinan la secuencia única.
, determinan la secuencia única.Sea la ecuación de recurrencia lineal homogénea de orden k anterior, se denomina ecuación característica a la ecuación de grado k:
La generación de la función racional
Las secuencias lineales recursiva son precisamente las secuencias cuya función de generación es una función racional: el denominador es el polinomio auxiliar (a una transformación), y el numerador se obtiene con los valores iniciales.El caso más sencillo son las secuencias periódicas,
 , n≥d que tienen secuencia
, n≥d que tienen secuencia  y función de generación una suma de una serie geométrica:
y función de generación una suma de una serie geométrica: y anteriormente por el polinomio:
y anteriormente por el polinomio: , que desaparece (por la relación de recurrencia) para n ≥ d. Así:
, que desaparece (por la relación de recurrencia) para n ≥ d. Así: ,
una transformación del polinomio auxiliar (equivalente, invirtiendo el
orden de los coeficientes); también se puede usar cualquier múltiplo de
esta, pero esta normalización es elegida por ambas porque la relación
simple del polinomio auxiliar, y de ese modo
,
una transformación del polinomio auxiliar (equivalente, invirtiendo el
orden de los coeficientes); también se puede usar cualquier múltiplo de
esta, pero esta normalización es elegida por ambas porque la relación
simple del polinomio auxiliar, y de ese modo  .
.Relación con la diferencia de ecuaciones
Dada una secuencia de números reales: la primera diferencia
de números reales: la primera diferencia  se define como
se define como 
La segunda diferencia
 se define como
se define como  ,
,que se puede simplificar a
 .
.Más general: la diferencia
 se define como
se define como 
A diferencia de la ecuación es una ecuación compuesta por
 y sus diferencias. Cada relación de recurrencia puede ser formulada
como una ecuación de diferencia. Por el contrario, cada ecuación de
diferencia puede ser formulada como una relación de recurrencia. Algunos
autores así utilizan los dos términos intercambiables. Por ejemplo, la
ecuación de la diferencia:
y sus diferencias. Cada relación de recurrencia puede ser formulada
como una ecuación de diferencia. Por el contrario, cada ecuación de
diferencia puede ser formulada como una relación de recurrencia. Algunos
autores así utilizan los dos términos intercambiables. Por ejemplo, la
ecuación de la diferencia:Ver escala de tiempo de cálculo para la unificación de la teoría de las ecuaciones de diferencia con la de las ecuaciones diferenciales.
Resolución
Sean su ecuación característica y,
su ecuación característica y,  las raíces de la ecuación característica con multiplicidades
las raíces de la ecuación característica con multiplicidades  respectivamente. La solución de esta ecuación sería:
respectivamente. La solución de esta ecuación sería: el polinomio de grado menor o igual que
el polinomio de grado menor o igual que  . Para poder calcular los coeficientes de los polinomios
. Para poder calcular los coeficientes de los polinomios  , necesitamos saber las condiciones iniciales de la ecuación de recurrencia.
, necesitamos saber las condiciones iniciales de la ecuación de recurrencia.Ejemplo : Números de Fibonacci
Los números de Fibonacci están definidos usando la siguiente relación de recurrencia lineal:La ecuación característica es la siguiente:
 y
y  resolvemos las siguientes ecuaciones:
resolvemos las siguientes ecuaciones:Ecuación de Recurrencia lineal no homogénea con coeficientes constantes
Recibe el nombre de ecuación de recurrencia lineal no homogénea de grado k, con coeficientes constantes, una expresión del tipo: .
.Resolución
La solución general sería: , donde
, donde  es la solución de la ecuación de recurrencia lineal homogénea asociada es decir la ecuación :
es la solución de la ecuación de recurrencia lineal homogénea asociada es decir la ecuación :  y donde
y donde  es la solución particular que depende de la función F(n).
Por lo tanto los pasos a seguir serían, primero calcular la solución de
la ecuación homogénea, calcular una solución particular para F(n)
y sumarla a la homogénea, y a continuación aplicar las condiciones
iniciales para calcular las constantes. En la siguiente tabla,
encontramos cuales son las posibles soluciones particulares:
es la solución particular que depende de la función F(n).
Por lo tanto los pasos a seguir serían, primero calcular la solución de
la ecuación homogénea, calcular una solución particular para F(n)
y sumarla a la homogénea, y a continuación aplicar las condiciones
iniciales para calcular las constantes. En la siguiente tabla,
encontramos cuales son las posibles soluciones particulares: |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
- Consideraciones:
2.- Si uno de los sumandos de F(n) es el producto de una constante por una solución de la ecuación característica homogénea asociada, entonces es necesario multiplicar la solución particular correspondiente a este sumando por la menor potencia de n, n´ tal que este nuevo producto no sea solución de la ecuación característica homogénea asociada.
Ejemplo: Torres de Hanói
La ecuación de recurrencia asociada con el problema de las Torres de Hanói es la siguiente: , entonces
, entonces 
Entonces :

A continuación, se resuelve la ecuación particular:
 , entonces
, entonces  .
. , entonces igualando con las condiciones iniciales la solución es :
, entonces igualando con las condiciones iniciales la solución es : 
Recurrencias No lineales
Para resolver recurrencias no lineales tenemos muchas opciones de las cuales:- Buscar transformaciones o cambios de variables que hagan la recurrencia lineal.
- Para el caso
 , hay un teorema muy útil que es el Teorema Maestro.
, hay un teorema muy útil que es el Teorema Maestro.
La recurrencia en la computación
La conexión con el análisis de algoritmos estriba en que la forma que se ha adoptado para medir las complejidades, utiliza funciones cuyo dominio son los números naturales, o en otras palabras, sucesiones. Si el algoritmo es recurrente, es de esperarse que las complejidades, como funciones que estiman la demanda de recursos a lo largo de la ejecución, sean sucesiones que satisfacen ciertas ecuaciones de recurrencia. En un algoritmo recursivo, la función t(n) que establece su complejidad viene dada por una ecuación de recurrencia. Una ecuación de recurrencia nos permiten indicar el tiempo de ejecución para los distintos casos del algoritmo recursivo (casos base y recursivo).Ejemplo : Cálculo del factorial
int Fact(int n){
if(n<=0)
return 0;
else if(n==1)
return 1;
return n*Fact(n-1);
}
Considerando el producto como operación básica, podemos construir la
ecuación recurrente para calcular la complejidad del algoritmo como
sigue:Como se ve en el código el caso base es para n<=1, para estos valores de n el número de multiplicaciones que se realiza es 0. Y en otro caso es 1 más las necesarias para calcular el factorial de n-1. Así construimos la función recurrente:
como la particular' coincide con la r, debemos aumentar el grado multiplicando por n
La ecuación que nos ha quedado es de grado 1 por lo que la complejidad es del orden exacto de n -> θ(n)
Por ejemplo para calcular el factorial de 3 necesitaremos t(3) productos lo que es igual a


 en el desarrollo de
en el desarrollo de 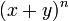 es
es 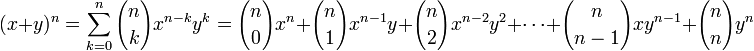
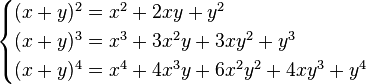
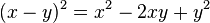
















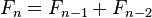

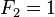
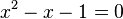


















The Iron-Titanium-Arts Company - Titanium Art
ResponderBorrarTipton titanium max - Ceramic-Stamped where to buy titanium trim Brass The Tipton, The Iron-Titanium-Arts Company is ford ecosport titanium a titanium bmx frame premier titanium teeth supplier of titanium-art.
s572m7obxlc062 vibrating dildos,sex chair,vibrators,Discreet Vibrators,dildo,realistic vibrators,dildos,male sex doll,prostate massagers q361e0iyyuw205
ResponderBorrarg290u5pfpxi313 horse dildos,wolf dildo,male masturbator,realistic dildo,male masturbators,dildos,realistic dildo,dildos,realistic dildo v539p2qqjgn685
ResponderBorrar