Función de distribución
Función de Distribución Acumulativa para la distribución normal en la siguiente imagen.
Función de Densidad de Probabilidad para varias distribuciones normales.
El trazo rojo distingue la distribución normal estándar.
Intuitivamente, asumiendo la función f como la ley de distribución de probabilidad, la fda sería la función con la recta real como dominio, con imagen del área hasta aquí de la función f, siendo aquí el valor x para la variable aleatoria real X.
La fda asocia a cada valor x, la probabilidad del evento: "la variable X toma valores menores o iguales a x".
Las Funciones de Distribución Acumulativa se emplean también para especificar la distribución de variables aleatorias multivariantes
Combinaciones y permutaciones
Normalmente usamos la palabra "combinación" descuidadamente, sin pensar en si el orden de las cosas es importante. En otras palabras:| "Mi ensalada de frutas es una combinación de manzanas, uvas y bananas": no importa en qué orden pusimos las frutas, podría ser "bananas, uvas y manzanas" o "uvas, manzanas y bananas", es la misma ensalada. | |
| "La combinación de la cerradura es 472": ahora sí importa el orden. "724" no funcionaría, ni "247". Tiene que ser exactamente 4-7-2. |
| Si el orden no importa, es una combinación. | |
| Si el orden sí importa es una permutación. |
 |
¡Así que lo de arriba se podría llamar "cerradura de permutación"! |
Una permutación es una combinación ordenada.
| Para ayudarte a recordar, piensa en "Permutación... Posición" |
Permutaciones
Hay dos tipos de permutaciones:- Se permite repetir: como la cerradura de arriba, podría ser "333".
- Sin repetición: por ejemplo los tres primeros en una carrera. No puedes quedar primero y segundo a la vez.
1. Permutaciones con repetición
Son las más fáciles de calcular. Si tienes n cosas para elegir y eliges r de ellas, las permutaciones posibles son:
n × n × ... (r veces) = nr
(Porque hay n posibilidades para la primera elección, DESPUÉS hay n posibilidades para la segunda elección, y así.)Por ejemplo en la cerradura de arriba, hay 10 números para elegir (0,1,...,9) y eliges 3 de ellos:
10 × 10 × ... (3 veces) = 103 = 1000 permutaciones
Así que la fórmula es simplemente:| nr |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden importa) |
2. Permutaciones sin repetición
En este caso, se reduce el número de opciones en cada paso. |
Por ejemplo, ¿cómo podrías ordenar 16 bolas de billar? Después de elegir por ejemplo la "14" no puedes elegirla otra vez. |
16 × 15 × 14 × 13 ... = 20,922,789,888,000
Pero a lo mejor no quieres elegirlas todas, sólo 3 de ellas, así que sería solamente:
16 × 15 × 14 = 3360
Es decir, hay 3,360 maneras diferentes de elegir 3 bolas de billar de entre 16.¿Pero cómo lo escribimos matemáticamente? Respuesta: usamos la "función factorial"
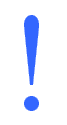 |
La función factorial (símbolo: !) significa que se multiplican números descendentes. Ejemplos:
|
| Nota: en general se está de acuerdo en que 0! = 1. Puede que parezca curioso que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas ecuaciones. | |
16! = 20,922,789,888,000
Pero si sólo quieres elegir 3, tienes que dejar de multiplicar
después de 14. ¿Cómo lo escribimos? Hay un buen truco... dividimos entre
13!...
16 × 15 × 14 × 13 × 12 ...
|
= 16 × 15 × 14 = 3360 | |
13 × 12 ...
|
La fórmula se escribe:
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden importa) |
Ejemplos:
Nuestro "ejemplo de elegir en orden 3 bolas de 16" sería:| 16! | = | 16! | = | 20,922,789,888,000 | = 3360 |
| (16-3)! | 13! | 6,227,020,800 |
| 10! | = | 10! | = | 3,628,800 | = 90 |
| (10-2)! | 8! | 40,320 |
(que es lo mismo que: 10 × 9 = 90)
Notación
En lugar de escribir toda la fórmula, la gente usa otras notaciones como:Combinaciones
También hay dos tipos de combinaciones (recuerda que ahora el orden no importa):- Se puede repetir: como monedas en tu bolsillo (5,5,5,10,10)
- Sin repetición: como números de lotería (2,14,15,27,30,33)
1. Combinaciones con repetición
En realidad son las más difíciles de explicar, así que las dejamos para luego.2. Combinaciones sin repetición
Así funciona la lotería. Los números se eligen de uno en uno, y si tienes los números de la suerte (da igual el orden) ¡entonces has ganado!La manera más fácil de explicarlo es:
- imaginemos que el orden sí importa (permutaciones),
- después lo cambiamos para que el orden no importe.
Ya sabemos que 3 de 16 dan 3360 permutaciones.
Pero muchas de ellas son iguales para nosotros, porque no nos importa el orden.
Por ejemplo, digamos que se tomaron las bolas 1, 2 y 3. Las posibilidades son:
| El orden importa | El orden no importa |
| 1 2 3 1 3 2 2 1 3 2 3 1 3 1 2 3 2 1 |
1 2 3 |
De hecho hay una manera fácil de saber de cuántas maneras "1 2 3" se pueden ordenar, y ya la sabemos. La respuesta es:
3! = 3 × 2 × 1 = 6
(Otro ejemplo: 4 cosas se pueden ordenar de 4! = 4 × 3 × 2 × 1 = 24 maneras distintas, ¡prueba tú mismo!)Así que sólo tenemos que ajustar nuestra fórmula de permutaciones para reducir por las maneras de ordenar los objetos elegidos (porque no nos interesa ordenarlos):
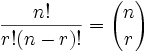 |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (No se puede repetir, el orden no importa) |
Notación
Además de los "grandes paréntesis", la gente también usa estas notaciones: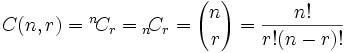
Ejemplo
| 16! | = | 16! | = | 20,922,789,888,000 | = 560 |
| 3!(16-3)! | 3!×13! | 6×6,227,020,800 |
| 16×15×14 | = | 3360 | = 560 |
| 3×2×1 | 6 |
Así que recuerda, haz las permutaciones, después reduce entre "r!"
... o mejor todavía...
¡Recuerda la fórmula!
Es interesante darse cuenta de que la fórmula es bonita y simétrica: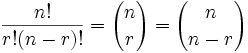
| 16! | = | 16! | = | 16! | = 560 |
| 3!(16-3)! | 13!(16-13)! | 3!×13! |
Triángulo de Pascal
Puedes usar el triángulo de Pascal para calcular valores. Baja a la fila "n" (la de arriba es n=0), y ve a la derecha "r" posiciones, ese valor es la respuesta. Aquí tienes un trozo de la fila 16:1 14 91 364 ... 1 15 105 455 1365 ... 1 16 120 560 1820 4368 ...
1. Combinaciones con repetición
OK, ahora vamos con este... |
Digamos que tenemos cinco sabores de helado: banana, chocolate, limón, fresa y vainilla. Puedes tomar 3 paladas. ¿Cuántas variaciones hay? Vamos a usar letras para los sabores: {b, c, l, f, v}. Algunos ejemplos son
|
(Y para dejarlo claro: hay n=5 cosas para elegir, y eliges r=3 de ellas.
El orden no importa, ¡y sí puedes repetir!)
Bien, no puedo decirte directamente cómo se calcula, pero te voy a enseñar una técnica especial para que lo averigües tú mismo. El orden no importa, ¡y sí puedes repetir!)
| Imagina que el helado está en contenedores, podrías decir "sáltate el primero, después 3 paladas, después sáltate los 3 contenedores siguientes" ¡y acabarás con 3 paladas de chocolate! | |
| Entonces es como si ordenaras a un robot que te trajera helado, pero no cambia nada, tendrás lo que quieres. |
Entonces los tres ejemplos de arriba se pueden escribir así:
| {c, c, c} (3 de chocolate): | |
| {b, l, v} (uno de banana, uno de limón y uno de vainilla): | |
| {b, v, v} (uno de banana, dos de vainilla): |
Fíjate en que siempre hay 3 círculos (3 paladas de helado) y 4 flechas (tenemos que movernos 4 veces para ir del contenedor 1º al 5º).
Así que (en general) hay r + (n-1) posiciones, y queremos que r de ellas tengan círculos.
Esto es como decir "tenemos r + (n-1) bolas de billar y queremos elegir r de ellas". Es decir, es como el problema de elegir bolas de billar, pero con números un poco distintos. Lo podrías escribir así:
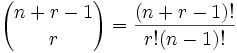 |
| donde n es el número de cosas que puedes elegir, y eliges r de ellas (Se puede repetir, el orden no importa) |
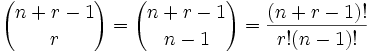
| (5+3-1)! | = | 7! | = | 5040 | = 35 |
| 3!(5-1)! | 3!×4! | 6×24 |
PERMUTACIONES Y COMBINACIONES
GENERALIZADAS
Teorema:
Supóngase que una sucesión S de n objetos tien n1 objetos idénticos del tipo 1, n2 objetos idénticos del tipo 2, . . . , nt objetos idénticos del tipo t. Entonces el número de ordenaciones de S es:
Supóngase que una sucesión S de n objetos tien n1 objetos idénticos del tipo 1, n2 objetos idénticos del tipo 2, . . . , nt objetos idénticos del tipo t. Entonces el número de ordenaciones de S es:
Demostración:
Se asignan las posiciones de cada uno de los n objetos para crear un orden de S. Es posible asignar las posiciones de los n1 objetos del tipo 1 en C(n, n1) formas. Una vbez realizada estas asignación, pueden asignarse las posiciones de los n2 objetos del tipo 2 en C(n - n1, n2) maneras, etc. Por lo tanto
Se asignan las posiciones de cada uno de los n objetos para crear un orden de S. Es posible asignar las posiciones de los n1 objetos del tipo 1 en C(n, n1) formas. Una vbez realizada estas asignación, pueden asignarse las posiciones de los n2 objetos del tipo 2 en C(n - n1, n2) maneras, etc. Por lo tanto
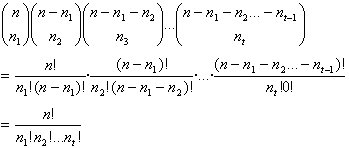
a) ¿De cuántas maneras es posible ordenar las siguiente letras ?
MISSISSIPPI
Debido a la repetición de algunas letras, la respuesta
no es 11!, pero si un número menor a 11!.
Consideremos el problema de llenar 11 espacios en blanco
_ _ _ _ _ _ _ _ _ _ _
con las letras dadas. Hay 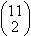 maneras de escoger posiciones para las dos letras P. Una vez seleccionadas las
dos P, existen
maneras de escoger posiciones para las dos letras P. Una vez seleccionadas las
dos P, existen 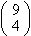 manera de elegir
posiciones para las cuatro S. Una vez seleccionas las posiciones para las letars
S, hay
manera de elegir
posiciones para las cuatro S. Una vez seleccionas las posiciones para las letars
S, hay 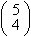 maneras de escoger lugares
para las letras I. Una vez realizadas estas elecciones, quesa un único
lugar para ser llenado por la letra M. Por el Teorema anterior, directamente
existen
maneras de escoger lugares
para las letras I. Una vez realizadas estas elecciones, quesa un único
lugar para ser llenado por la letra M. Por el Teorema anterior, directamente
existen 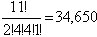 maneras de ordenar dichas
letras.
maneras de ordenar dichas
letras.
b) De cuántos modos se pueden repartir ocho libros distintos
entre tres estudiantes si Guillermo recibe cuatro libros, en tanto que Maria
y Silvia reciben 2 cada una.
Sea G = Guillermo, S = Sofia y M = Maria.
Unos ejemplos de ordenación serian GGGGSSMM, GGGSMGMS,
MMSSGGGG, etc.
Cada uno de estos ordenamientos determina una distribución
de libros. Por lo que existen 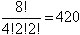 maneras de repartir los libros.
maneras de repartir los libros.
c) ¿De cuantas maneras pueden formarse tres comités
distintos de un grupo de 20 personas, si los comités deben tner 3, 5
y 7 personas respectivamente?
La respuesta es 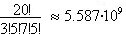
d) Una partida de Bridge es una partición ordenada de
52 cartas que comprende 4 conjuntos de 13 cartas cada uno. Por lo tanto hay
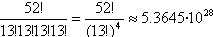 partidas de Bridge.
partidas de Bridge.
e) ¿De cuántas maneras posibles pueden distribuirse
12 estudiantes en 3 grupos, con 4 estudiantes cada grupo, de manera que un grupo
estudie un tema, el otro un tema diferente y el tercero otro diferente a los
dos anteriores?
En total hay 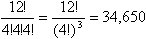 posibles maneras de distribuir a los estudiantes.
posibles maneras de distribuir a los estudiantes.
f) ¿De cuántas maneras pueden distribuirse 19 estudiantes
en 5 grupos, 2 grupos de 5 y 3 grupos de 3, de manera que cada grupo estudie
un tema distinto?
En total hay 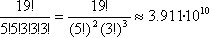 posibles maneras de distribuir a los estudiantes.
posibles maneras de distribuir a los estudiantes.
g) ¿De cuantás formas es posible hacer una partición
de un conjunto de 100 elementos en 50 conujuntos diferentes de 2 elementos cada
uno?
La respuest es 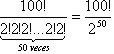 formas
posibles.
formas
posibles.
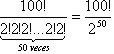 formas
posibles.
formas
posibles.
De forma más general puede enunciarse el mismo problema
de la siguiente manera ¿De cuántas formas es posible hacer una
partición de un conjunto conm 2n elementos en n conjuntos
de 2 elelmentos cada uno?.
Entonces la respuesta es 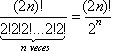 formas
posibles.
formas
posibles.
Teorema: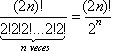 formas
posibles.
formas
posibles. Si X es un conjunto que contiene n elementos, entonces el número de selecciones de r elementos, no ordenadas, con repeticiones permitidas y tomando del conjunto X es:
NOTA:
Es posible que r sea mayor que n cuando se permiten repeticiones.
Ejemplos:Es posible que r sea mayor que n cuando se permiten repeticiones.
a) Supongase que se tienen 3 pilas de pelotas rojas, azules y verdes y cada una contiene al menos 8 pelotas.
i) ¿De cuántos modos se pueden seleccionar 8 pelotas?
ii) ¿De cuántas maneras de pueden seleccionar 8 pelotas si se debe tener al menos una de cada color?
Por el Teorema anterior, el número de formas para elegir
8 pelotas es 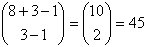 .
.
También se puede aplicar el Teorema para resolver la parte
ii). Si se selecciona una pelota de cada color. Para completar la elección,
deben escogerse 5 pelotas más. Esto se puede hacer de 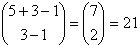 formas diferentes.
formas diferentes.
b)¿De cuántas maneras es posible colocar 10 canicas
rojas en 5 bolsas?
La respuesta es 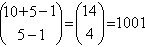 maneras posibles.
maneras posibles.
c) ¿De cuántas maneras es posible seleccionar 10
monedas de un abasto ilimitado de monedas de cincuenta, cien, doscientos y quinientois
pesos?
Entonces es posible seleccionar 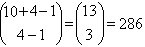 formas distintas.
formas distintas.
d) De cuántas formas pueden distribuirse 12 libros idénticos
de matemáticas discretas entre 4 estudiantes.
En total se pueden distribuir 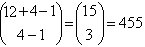 formas diferentes.
formas diferentes.
e) Cuántas soluciones enteras no negativas tiene la ecuación
x1 + x2 +x3 + x4
= 29
Cada solución es equivalente a elegir 29 elementosm xi
del tipo i, i = 1, 2, 3, 4.El número solución es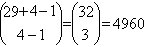 .
.
f) Una tienda ofrece 20 tipos de donas. Si suponemos que al menos
hay una docena de cada tipo cuando entramos a la tienda, podemos elegir una
docena de donas de 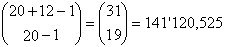 opciones posibles.
opciones posibles.


Gracias me sirvio mucho para mi tarea :)
ResponderBorrar