Coeficiente binomial
Los coeficientes binomiales, números combinatorios o combinaciones son números estudiados en combinatoria
que corresponden al número de formas en que se pueden extraer
subconjuntos a partir de un conjunto dado. Sin embargo, dependiendo del
enfoque que tenga la exposición, se pueden usar otras definiciones
equivalentes.
Definición combinatoria
 , pues hay 10 formas de escoger (en rojo) 3 objetos a partir de un conjunto con 5 elementos
, pues hay 10 formas de escoger (en rojo) 3 objetos a partir de un conjunto con 5 elementos| A,B | A,C | A,D | A,E | A,F |
| B,C | B,D | B,E | B,F | |
| C,D | C,E | C,F | ||
| D,E | D,F | |||
| E,F |
 ,
,  ,
, 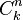 , o
, o  .
Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que
hay 15 formas de escoger 2 objetos a partir de un conjunto con 6
elementos.
.
Así, en el ejemplo anterior se tiene entonces que C(6,2)=15, puesto que
hay 15 formas de escoger 2 objetos a partir de un conjunto con 6
elementos.Los números C(n,k) se conocen como «coeficientes binomiales», pero es frecuente referirse a ellos como «combinaciones de n en k», o simplemente «n en k». Por tanto, la primera definición es:
El coeficiente binomial |
Definición algebraica
Hay 5×4×3 formas de escoger ordenadamente 3 objetos de un conjunto con 5.
Supongamos que el conjunto original tiene 5 elementos, de los cuales se deben escoger 3. Al momento de escoger el primero, se tiene 5 opciones disponibles, pero una vez fijo el primero, sólo hay 4 opciones para el segundo, y por tanto sólo 3 opciones para el último (pues no se puede repetir los escogidos en los primeros 2 pasos). De este modo, la selección puede hacerse de 5×4×3=60 formas.
Sin embargo, en tal conteo, el orden en que se escogen los elementos hace diferencia. Por ejemplo, tomar C, luego B, luego E, es una selección diferente de tomar B, luego C y luego E. Pero en la definición de coeficiente binomial, no importa el orden en que se eligen los objetos, únicamente cuáles se escogen. Por tanto, las elecciones BCE, BEC, CEB, CBE, ECB y EBC son todas equivalentes. Del mismo modo, las elecciones ABC, ACB, BCA, BAC, CAB y CBA son equivalentes, y así para cualquier terna de letras.
De esta forma, el resultado obtenido (60) no es la cantidad de subconjuntos de 3 elementos de {A,B,C,D,E}, sino que cada subconjunto está contado 6 veces, por lo que la cantidad de subconjuntos es realmente 60/6 = 10.
El argumento presentado para el ejemplo puede generalizarse de la siguiente forma. Si se tiene un conjunto con n elementos, de los cuales se van a escoger k de ellos, la elección (ordenada) puede hacerse de
- n × (n-1) × (n-2) ×... × (n-k+1)
Ahora, hay que dividir el producto anterior entre el número de selecciones «equivalentes». Pero si se tiene k objetos, hay k! formas de permutarlos, es decir, k! formas de listarlos en distinto orden. Recordemos que k! se lee k-factorial y es igual a
- k! = 1×2×3×...× k
 .
.
El coeficiente binomial |

Teorema del binomio
En matemática, el teorema del binomio
es una fórmula que proporciona el desarrollo de la potencia n-ésima de n
(siendo n, entero positivo) de un binomio. De acuerdo con el teorema,
es posible expandir la potencia (x + y)n en una suma que implica términos de la forma axbyc, donde los exponentes b y c son números naturales con b + c = n, y el coeficiente a de cada término es un número entero positivo que depende de n y b. Cuando un exponente es cero, la correspondiente potencia es usualmente omitida del término. Por ejemplo,
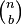 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).
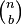 o
o  (los dos tienen el mismo valor).
(los dos tienen el mismo valor).Formulación del teorema
Este teorema establece: Usando la fórmula para calcular el valor de (que también es representado ocasionalmente como
(que también es representado ocasionalmente como  o
o 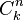 ) se obtiene la siguiente representación:
) se obtiene la siguiente representación:El coeficiente de |
 recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:
recibe el nombre de coeficiente binomial y representa el número de formas de escoger k elementos a partir de un conjunto con n elementos. Usualmente el teorema del binomio se expresa en la siguiente variante:Ejemplo
Como ejemplo, para n=2, n=3, n=4, utilizando los coeficientes del triángulo de Pascal:(2)Para obtener la expansión de las potencias de una resta, basta con tomar -y en lugar de y en los términos con potencias impares de y. La expresión (2) queda de la siguiente forma:



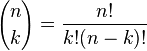


 en el desarrollo de
en el desarrollo de 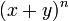 es
es 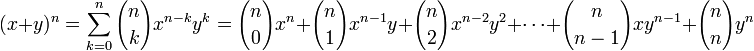
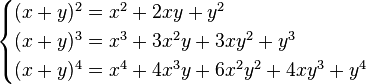
No hay comentarios.:
Publicar un comentario