Conjuntos

Fórmula bien formada

En lógica matemática, una fórmula bien formada, también llamada expresión bien formada, y a menudo abreviada fbf o EBF, es una cadena de caracteres o palabra generada según una gramática formal a partir de un alfabeto dado. Un lenguaje formal se define como el conjunto de todas sus fórmulas bien formadas.

 

1. Una letra enunciativa es una fbf.
2. Toda fbf a la cual se antepone el símbolo "¬" (negación) es una fbf.
3. Si A y B son fbfs, entonces también lo son las secuencias: (AB), (AB), (AB),y (AB)
4. Toda secuencia de caracteres producida por la aplicación de los pasos 1, 2, 3, en cualquier orden, constituye una fbf. (Cláusula de recursión)
5. Ninguna otra secuencia constituye una fbf. (Cláusula de exclusión) .

Teoría de conjuntos

  Un conjunto es la reunión en un todo de objetos bien definidos y diferenciables entre si, que se llaman elementos del mismo.

Si a es un elemento del conjunto A se denota con la relación de pertenencia a Î A.
En caso contrario, si a no es un elemento de A se denota aÏ A.
 
Ejemplos de conjuntos:

• Æ : el conjunto vacío, que carece de elementos.
• N: el conjunto de los números naturales.
• Z: el conjunto de los números enteros.
• Q : el conjunto de los números racionales.
• R: el conjunto de los números reales.
• C: el conjunto de los números complejos.

 
Se puede definir un conjunto:

• por extensión, enumerando todos y cada uno de sus elementos.
• por comprensión, diciendo cuál es la propiedad que los caracteriza.

 
Un conjunto se suele denotar encerrando entre llaves a sus elementos, si se define por extensión,
o su propiedad característica, si se define por comprensión. Por ejemplo:

• A := {1,2,3, ... ,n}
• B := {pÎ Z | p es par}

 
Se dice que A está contenido en B (también que A es un subconjunto de B o que A es una parte de B),
y se denota A Í B, si todo elemento de A lo es también de B, es decir, a Î A Þ a Î B. Dos conjuntos A y B se dicen iguales, y se denota A = B, si simultáneamente A Í B y B Í A;
esto equivale a decir que tienen los mismos elementos (o también la misma propiedad característica).
Para cualquier conjunto A se verifica que ÆÍ A y A Í A;
B Í A es un subconjunto propio de A si A ¹ Æ y B ¹ A.
El conjunto formado por todos los subconjuntos de uno dado A se llama partes de A, y se denota à (A).
Entonces, la relación B Í A es equivalente a decir B Î Ã (A). Ejemplos:
 
Si A = {a,b} entonces à (A) = {Æ ,{a},{b},A}. Si a Î A entonces {a} Îà (A).
Cuando en determinado contexto se consideran siempre conjuntos que son partes de uno dado U,
se suele considerar a dicho U como conjunto universal o de referencia.

OPERACIONES ENTRE CONJUNTOS

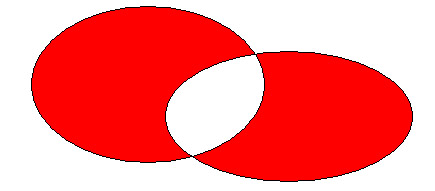
Dados dos conjuntos A y B, se llama diferencia al conjunto A - B := {a Î A | a Ï B}.
Asimismo, se llama diferencia simétrica entre A y B al conjunto A D B := (A - B) È (B - A). Si A Î Ã (U), a la diferencia U - A se le llama complementario de A respecto de U,
y se denota abreviadamente por A' (U se supone fijado de antemano).
Es fácil ver que si A y B son subconjuntos cualesquiera de U se verifica:

• Æ ' = U .
• U ' = Æ .
• (A')' = A .
• A Í B Û B' Í A' .
• Si A = { x Î U | p(x) es una proposición verdadera} entonces A' = { x Î U | p(x) es una proposición falsa}.

 
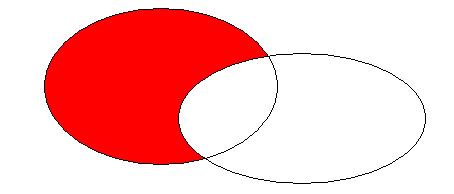
Se llama unión de dos conjuntos A y B al conjunto formado por objetos que son elementos de A o de B,
es decir: A È B := { x | x Î A Ú x Î B}. Se llama intersección de dos conjuntos A y B al conjunto formado por objetos que son elementos de A y de B,
es decir: A Ç B := {x | x Î A Ù x Î B}.
Si A y B son subconjuntos de un cierto conjunto universal U, entonces es fácil ver que A - B = A Ç B'.
En este caso, la llamadas operaciones booleanas (unión e intersección) verifican las siguientes propiedades :

PROPIEDADES	UNION	INTERSECCION
1.- Idempotencia	A È A = A	A Ç A = A
2.- Conmutativa	A È B = B È A	A Ç B = B Ç A
3.- Asociativa	A È ( B È C ) = ( A È B ) È C	A Ç ( B Ç C ) = ( A Ç B ) Ç C
4.- Absorción	A È ( A Ç B ) = A	A Ç ( A È B ) = A
5.- Distributiva	A È ( B Ç C ) = ( A È B ) Ç ( A È C )	A Ç ( B È C ) = ( A Ç B ) È ( A Ç C )
6.- Complementariedad	A È A' = U	A Ç A' = Æ

 
Estas propiedades hacen que partes de U con las operaciones unión e intersección tenga una estructura de álgebra de Boole.
Además de éstas, se verifican también las siguientes propiedades:

• A È Æ = A , A Ç Æ = Æ ( elemento nulo ).
• A È U = U , A Ç U = A ( elemento universal ).
• ( A È B )' = A' Ç B' , ( A Ç B )' = A' È B' ( leyes de Morgan ).

 
Dados dos conjuntos A y B, se define el producto cartesiano de ambos como el conjunto de pares ordenados:
  A ´ B := { (a,b) : a Î A Ù b Î B}
Dos pares (a,b) y (c,d) de A ´ B son iguales si a = c y b = d; análogamente, dados cuatro conjuntos A,B,C,D se verifica
 
A ´ B = C ´ D Û ( A = C Ù B = D )
Se llama grafo relativo a A ´ B a todo subconjunto G Í A ´ B.
Dado un grafo G relativo a A ´ B, se llama proyección de G sobre A al conjunto
 
Proy_AG := { a Î A : (a,b) Î G, $ b Î B}
Análogamente se define la proyección Proy_BG de G sobre B.
Por último, los conceptos anteriores pueden generalizarse a familias de conjuntos.
Si para cada elemento i de un conjunto (de índices ) I se tiene un conjunto A_i , entonces se define el conjunto { A_i : i Î I }
y se denomina familia de conjuntos indicada por I. También se suele denotar por { A_i } _{i Î I} .
De forma análoga se define una familia de elementos ( a_i ) _{i Î I} .
Dada una familia de conjuntos { A_i } _{i Î I} se definen:
 

• È _{i ÎI} A_i := { a : a Î A_i , $ i Î I }
• Ç _{i Î I} A_i := { a : a Î A_i , " i Î I }
• Õ _{i Î I} A_i := { (a_i) : a_i Î A_i , " i Î I }

 
Las propiedades de la unión e intersección siguen siendo válidas para familias de conjuntos, y en particular las leyes de Morgan :
  ( È _{i Î I} A_i )' = Ç _{i Î I} A'_i     ,    (Ç_{i Î I} A_i )' = È_{i Î I} A'_i DIAGRAMAS DE VENN Los conjuntos de suelen representar gráficamente mediante "diagramas de Venn", con una línea que encierra a sus elementos.
Así, todas las operaciones entre conjuntos se pueden representar gráficamente con el fin de obtener una idea más intuitiva.
A Í B

 
A È B

 
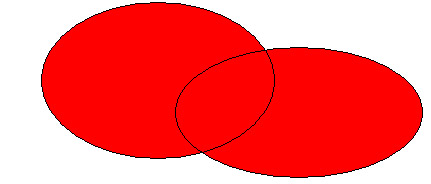
A Ç B

 
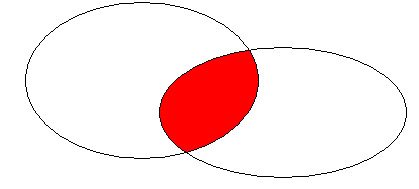
A - B

 
A D B

RELACION ENTRE LA TEORIA DE CONJUNTOS Y LA LOGICA PROPOSICIONAL

Existe una relación muy estrecha entre la Teoría de Conjuntos y la Lógica Proposicional.
Para mostrar dicha relación, denotemos por letras mayúsculas A,B ... los conjuntos y
por las correspondientes minúsculas a,b ... sus propiedades características
(es decir, la proposición lógica que caracteriza a los elementos de cada conjunto);
entonces se tiene la siguiente correspondencia:
 
 

conjuntos	A Í B	A = B	A È B	A Ç B	A'	A - B	A D B
proposiciones	a Þ b	a Û b	a Ú b	a Ù b	a'	a Ù b'	a Ú b

Además, el conjunto vacío se corresponde con una contradicción y el conjunto universal con una tautología.
Mediante esta correspondencia, todos los resultados sobre conjuntos se pueden reescribir en términos de lógica
proposicional y viceversa; a modo de ejemplo:
 
 

A È ( A Ç B ) = A	a Ú ( b Ù c ) Û a
A È ( B Ç C ) = ( A È B ) Ç ( A È C )	a Ú ( b Ù c ) Û ( a Ú b ) Ù ( a Ú c )
( A È B )' = A' Ç B'	( a Ú b )' Û a' Ù b'

PROPOSICIONES CON CUANTIFICADORES
Los símbolos " (cuantificador universal) y $ (cuantificador existencial) se utilizan en Matemáticas para
enunciar proposiciones logicas relativas a objetos matemáticos.
Sea A un conjunto y p(x) una proposición o propiedad que hace referencia a un elemento x.
(1) Cuantificador universal : La expresión
        " x Î A Þ p(x)
se lee "para todo x que pertenece a A se verifica p(x)", representa la proposición
        { x Î A : p(x) } = A
(2) Cuantificador existencial : La expresión
        $ x Î A | p(x)
se lee "existe x que pertenece a A tal que p(x)", representa la proposición
        { x Î A : p(x) } ¹ Æ
 
La negación de cualquiera de las dos proposiciones anteriores se realiza negando la proposición p(x)
y cambiando el cuantificador universal por el cuantificador existencial, o viceversa.
Así, la negación de la proposición "" x Î A Þ p(x)" es "$ x Î A | p(x)' ", mientras que
la negación de "$ x Î A | p(x)" es "" x Î A Þ p(x)' "
 
 

Conjuntos finitos : Combinatoria

La Combinatoria es la parte de las Matemáticas que se dedica al estudio de los conjuntos finitos.
Puesto que la propiedad principal de estos conjuntos es que se puede representar su número de elementos
mediante un número natural (llamado cardinal de dicho conjunto), la tarea básica de la Combinatoria es
precisamente el cálculo del cardinal de dichos conjuntos.
Para dicho cálculo se necesita definir los llamados números combinatorios:
 
        (1) Números factoriales: se define n! mediante la ley de recurrencia
                        n! = n · (n-1)!
                y la condición inicial 0! := 1. De forma iterativa, se tiene
                        n! = n · (n-1) · (n-2) · ... · 3 · 2 · 1
        n! es el número de permutaciones de n elementos, es decir, es el número total de formas de ordenar n elementos
        de todas las formas distintas posibles.
 
        (2) Coeficientes binomiales: se definen por la fórmula
                        
        El número "n sobre k" es el número de combinaciones de n elementos tomados de k en k, es decir,
        el número de subconjuntos distintos de k elementos que tiene un conjunto con n elementos.
        Los coeficientes binomiales tienen dos propiedades básicas:
                (a)
                        
                (b)
                        
 
        Como aplicación de los números combinatorios y del Binomio de Newton, podemos contar el número total de
        subconjuntos que tiene un conjunto A con n elementos, es decir, el cardinal de partes de A; para ello, notemos
        que el número de tales subconjuntos se obtiene sumando el número de subconjuntos de 0 elementos más los de
        1 elemento, más los de 2 elementos, y así hasta los de n elementos, es decir:
 
                        
 
        Pero esta cantidad corresponde a desarrollar mediante el binomio de Newton la expresión
                (1+1)ⁿ  = 2ⁿ
        Así pues se obtiene que # Ã (A) = 2ⁿ si # A = n.

 Sistemas numéricos
  
Un sistema numérico son un conjunto de símbolos y reglas que se utilizan para representar datos numéricos o cantidades. Se caracterizan por su base que indican el número de símbolos distinto que utiliza y además es el coeficiente que determina cual es el valor de cada símbolo dependiendo de la posición que ocupe. Estas cantidades se caracterizan por tener dígitos enteros y fraccionarios.
Si aj indica cualquier dígito de la cifra, b la base del sistema de numeración y además de esto la cantidad de dígitos enteros y fraccionarios son n y k respectivamente, entonces el número representado en cualquier base se puede expresar de la siguiente forma:
Nb = [an-1.an-2.an-3..........a3.a2.a1.a0,a-1.a-2.a-3 .......a-k]b
Donde: j = {n-1, n-2,.........2, 1, 0,-1, -2, ......, -k} y n + k indica la cantidad de dígitos de la cifra.
Por ejemplo, el número 31221, 324 en base cuatro tiene n=5 y k=2 con la parte entera: an-1=a4=3; a3=1; a2=2; a1=2; a0=1 y parte fraccionaria a-1=3; a-2=2
SISTEMA DECIMAL.
Este es el sistema que manejamos cotidianamente, está formado por diez símbolos {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} por lo tanto la base del sistema es diez (10).