Resolucion de problemas, diseño, de algoritmos, requieren un razonamiento logico. La logica trata los metodos y el arte del razonamiento sistematico.

LOGICA PROPORCIONAL.

Una proporsion es una sentencia declarativa que es verdadera o falsa pero no ambas por ejemplo:

"La mañana es fria"
"Un girasol es amarillo"

PROPOSICIONES COMPUESTAS.

Una proposicion es indivisible se conose como proposicion primitiva. Las sentencias derivadas de las primitivas y de varios conectores logicos como:

"no, y, o, si ... entonces, si y solo si"

Estas se conocen como proposiciones compuestas.
Ejemplo:

"una vibora no es viviparo"
"las hojas son rojas y azules"
"Comprarias fura o verduras"
"si te mojas entonces te enfermas"
"Un insecto vuela si o solo si tiene alas"

EJEMPLOS:

proposiciones compuestas:

Escojerias gastos o perros.
si tropiesas puedes caer
el transporte es caro.
el leon ataca si o solo si esta en peligro

proposiciones simples:

los autos son pesados
los boligrafos tienen tinta.
el pasto es verde.
los gatos son casadores

Tabla de verdad

Una tabla de verdad, o tabla de valores de verdad, es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de verdad que se pueda asignar.¹ Fue desarrollada por Charles Sanders Peirce por los años 1880, pero el formato más popular es el que introdujo Ludwig Wittgenstein en su Tractatus logico-philosophicus, publicado en 1921.

Definiciones en el cálculo lógico

Para establecer un Sistema formal se establecen las definiciones de los operadores. Las definiciones se harán en función del fin que se pretenda al construir el sistema que haga posible la formalización de argumentos:

Como razonamientos deductivos lógico-lingüísticos
Como construcción de un sistema matemático puro
Como una aplicación lógica en un Circuito de conmutación.

Verdadero

El valor verdadero se representa con la letra V; si se emplea notación numérica se expresa con un uno: 1; en un circuito eléctrico, el circuito está cerrado.

Falso

El valor falso se representa con la letra F; si se emplea notación numérica se expresa con un cero: 0; en un circuito eléctrico, el circuito está abierto.

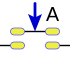
Variable

Para una variable lógica A, B, C, ... que pueden ser verdaderas V, o falsas F, los operadores fundamentales se definen así:

\begin{array}{|c|c|} \hline A & A \\ \hline V & V \\ F & F \\ \hline \end{array}

Negación

La negación es un operador que se ejecuta, sobre un único valor de verdad, devolviendo el valor contradictorio de la proposición considerada.

\begin{array}{|c|c|} \hline A & \thicksim A \\ \hline V & F \\ F & V \\ \hline \end{array}

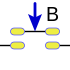
Conjunción

La conjunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones son verdaderas, y falso en cualquier otro caso. Es decir es verdadera cuando ambas son verdaderas
La tabla de verdad de la conjunción es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \and B \\ \hline V & V & V \\ V & F & F \\ F & V & F \\ F & F & F \\ \hline \end{array}

Que se corresponde con la columna 8 del algoritmo fundamental.
en simbologia "^" hace referencia a el conector "y"

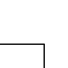
Disyunción

La disyunción es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando una de las proposiciones es verdadera, o cuando ambas lo son, y falso cuando ambas son falsas.
La tabla de verdad de la disyunción es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \or B \\ \hline V & V & V \\ V & F & V \\ F & V & V \\ F & F & F \\ \hline \end{array}

Que se corresponde con la columna 2 del algoritmo fundamental.

Implicación o Condicional

El condicional material es un operador que actúa sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de falso sólo cuando la primera proposición es verdadera y la segunda falsa, y verdadero en cualquier otro caso.
La tabla de verdad del condicional material es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \Rightarrow B \\ \hline V & V & V \\ V & F & F \\ F & V & V \\ F & F & V \\ \hline \end{array}

Que se corresponde con la columna 5 del algoritmo fundamental.

Equivalencia, doble implicación o Bicondicional

El bicondicional o doble implicación es un operador que funciona sobre dos valores de verdad, típicamente los valores de verdad de dos proposiciones, devolviendo el valor de verdad verdadero cuando ambas proposiciones tienen el mismo valor de verdad, y falso cuando sus valores de verdad son diferentes.
La tabla de verdad del bicondicional es la siguiente:

\begin{array}{|c|c|c|} \hline A & B & A \Leftrightarrow B \\ \hline V & V & V \\ V & F & F \\ F & V & F \\ F & F & V \\ \hline \end{array}

Que se corresponde con la columna 7 del algoritmo fundamental.

induccion matematica

la induccion es el razonamiento que permite demostrar una infinidad de proposiciones o una proposicion que depende de un parametro "n" que forma una infinidad de valores usualmente de los enteros naturales.

El número entero

a\,

tiene la propiedad

P\,

. El hecho de que cualquier número entero

n\,

también tenga la propiedad

P\,

implica que

n+1\,

también la tiene. Entonces todos los números enteros a partir de

a\,

tienen la propiedad

P\,

La demostración está basada en el axioma denominado principio de la inducción matemática.1
Se probará que la siguiente declaración P ( n ), que se supone válida para todos los números naturales n .

1 + 2 + \cdots + n = \frac{n(n + 1)}{2}\,.

P ( n ) da una fórmula para la suma de los números naturales menores o igual a n . La prueba de que P ( n ) es verdadera para todos los números naturales procede como sigue.
Base: Se muestra que es válida para n = 1.
con P(1) se tiene:

1 = \frac{1\cdot(1 + 1)}{2}\,.

En el lado izquierdo de la ecuación, el único término es 1, entonces su valor es 1.
mientras que el término derecho, 1·(1 + 1)/2 = 1.
Ambos lados son iguales, n = 1. Entonces P(1) es verdadera.

tautologia

En lógica, una tautología (del griego ταυτολογία, "decir lo mismo") es una fórmula bien formada de un sistema de lógica proposicional que resulta verdadera para cualquier interpretación; es decir, para cualquier asignación de valores de verdad que se haga a sus fórmulas atómicas.¹ ² La construcción de una tabla de verdad es un método efectivo para determinar si una fórmula cualquiera es una tautología o no.

Matematicas Discretas

martes, 1 de diciembre de 2015

Logica