Análisis de algoritmos
El
análisis de algoritmos
es una parte importante de la Teoría de complejidad computacional más
amplia, que provee estimaciones teóricas para los recursos que necesita
cualquier algoritmo
que resuelva un problema computacional dado. Estas estimaciones
resultan ser bastante útiles en la búsqueda de algoritmos eficientes.
A la hora de realizar un análisis teórico de algoritmos es común calcular su complejidad en un
sentido asintótico,
es decir, para un tamaño de entrada suficientemente grande. La cota
superior asintótica, y las notaciones omega (cota inferior) y theta
(caso promedio) se usan con esa finalidad. Por ejemplo, la búsqueda
binaria decimos que se ejecuta en una cantidad de pasos proporcional a
un logaritmo, en O(log(n)), coloquialmente "en tiempo logarítmico".
Normalmente las estimaciones asintóticas se utilizan porque diferentes
implementaciones
del mismo algoritmo no tienen por qué tener la misma eficiencia. No
obstante la eficiencia de dos implementaciones "razonables" cualesquiera
de un algoritmo dado están relacionadas por una constante
multiplicativa llamada
constante oculta.
La medida exacta
(no asintótica)
de la eficiencia a veces puede ser computada pero para ello suele hacer
falta aceptar supuestos acerca de la implementación concreta del
algoritmo, llamada modelo de computación. Un modelo de computación puede
definirse en términos de un ordenador abstracto, como la Máquina de
Turing,
y/o postulando que ciertas operaciones se ejecutan en una unidad de
tiempo. Por ejemplo, si al conjunto ordenado al que aplicamos una
búsqueda binaria
tiene 'n' elementos, y podemos garantizar que una única búsqueda
binaria puede realizarse en un tiempo unitario, entonces se requieren
como mucho log
2 N + 1 unidades de tiempo para devolver una respuesta.
Las
medidas exactas de eficiencia son útiles para quienes
verdaderamente implementan y usan algoritmos, porque tienen más
precisión y así les permite saber cuánto tiempo pueden suponer que
tomará la ejecución. Para algunas personas, como los desarrolladores de
videojuegos, una constante oculta puede significar la diferencia entre
éxito y fracaso.
Las estimaciones de tiempo dependen de cómo definamos un paso. Para
que el análisis tenga sentido, debemos garantizar que el tiempo
requerido para realizar un paso se encuentre acotado superiormente por
una constante. Hay que mantenerse precavido en este terreno; por
ejemplo, algunos análisis cuentan con que la suma de dos números se hace
en un paso. Este supuesto puede no estar garantizado en ciertos
contextos. Si por ejemplo los números involucrados en la computación
pueden ser arbitrariamente grandes, dejamos de poder asumir que la
adición requiere un tiempo constante (usando papel y lápiz, compara el
tiempo que necesitas para sumar dos enteros de 2 dígitos cada uno y el
necesario para hacerlo con dos enteros pero de 1000 dígitos cada uno).
Grafo
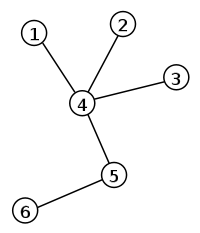
Grafo etiquetado con 6 vértices y 7 aristas.
En matemáticas y ciencias de la computación, un
grafo (del griego
grafos:
dibujo, imagen) es un conjunto de objetos llamados vértices o nodos
unidos por enlaces llamados aristas o arcos, que permiten representar
relaciones binarias entre elementos de un conjunto.
1 Son objeto de estudio de la teoría de grafos.
Típicamente, un grafo se representa gráficamente como un conjunto de puntos (vértices o nodos) unidos por líneas (aristas).
Desde
un punto de vista práctico, los grafos permiten estudiar las
interrelaciones entre unidades que interactúan unas con otras. Por
ejemplo, una red de computadoras puede representarse y estudiarse
mediante un grafo, en el cual los vértices representan terminales y las
aristas representan conexiones (las cuales, a su vez, pueden ser cables o
conexiones inalámbricas).
Prácticamente cualquier problema puede
representarse mediante un grafo, y su estudio trasciende a las diversas
áreas de las ciencias exactas y las ciencias sociales.
Historia y problema de los puentes de Königsberg

Los siete puentes de Königsberg.
El
primer artículo científico relativo a grafos fue escrito por el
matemático suizo Leonhard Euler en 1736. Euler se basó en su artículo en
el
problema de los puentes de Königsberg. La ciudad de Kaliningrado, originalmente
Königsberg, es famosa por sus siete puentes que unen ambas márgenes del río Pregel
con dos de sus islas. Dos de los puentes unen la isla mayor con la
margen oriental y otros dos con la margen occidental. La isla menor está
conectada a cada margen por un puente y el séptimo puente une ambas
islas. El problema planteaba lo siguiente: ¿es posible dar un paseo
comenzando desde cualquiera de estas regiones, pasando por todos los
puentes, recorriendo solo una vez cada uno y regresando al mismo punto
de partida?
Abstrayendo este problema y planteándolo con la (entonces aún básica)
teoría de grafos, Euler consigue demostrar que el grafo asociado al
esquema de puentes de Königsberg no tiene solución, es decir, no es
posible regresar al vértice de partida sin pasar por alguna arista dos
veces.
De hecho, Euler resuelve el problema más general: ¿qué condiciones
debe satisfacer un grafo para garantizar que se puede regresar al
vértice de partida sin pasar por la misma arista más de una vez? Si
definimos como «grado» al número de líneas que se encuentran en un punto
de un grafo, entonces la respuesta al problema es que
los puentes de un pueblo se pueden atravesar exactamente una vez si, salvo a lo sumo dos, todos los puntos tienen un grado par.
Definiciones
Un
grafo 
es un par ordenado

, donde:
 es un conjunto de vértices o nodos, y
es un conjunto de vértices o nodos, y es un conjunto de aristas o arcos, que relacionan estos nodos.
es un conjunto de aristas o arcos, que relacionan estos nodos.
Normalmente

suele ser finito. Muchos resultados importantes sobre grafos no son aplicables para
grafos infinitos.
Se llama
orden del grafo

a su número de vértices,

.
El grado de un vértice o nodo

es igual al número de arcos que lo tienen como extremo.
Un bucle es una arista que relaciona al mismo nodo; es decir, una arista donde el nodo inicial y el nodo final coinciden.
Dos o más aristas son paralelas si relacionan el mismo par de vértices.
Grafo no dirigido
Un
grafo no dirigido o
grafo propiamente dicho es un grafo

donde:
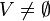
 es un conjunto de pares no ordenados de elementos de
es un conjunto de pares no ordenados de elementos de  .
.
Un
par no ordenado es un conjunto de la forma

, de manera que

. Para los grafos, estos conjuntos pertenecen al conjunto potencia de

, denotado
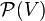
, y son de cardinalidad 2.
Grafo dirigido
Un
grafo dirigido o
digrafo es un grafo

donde:
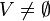
 es un conjunto de pares ordenados de elementos de
es un conjunto de pares ordenados de elementos de  .
.
Dada una arista

,

es su
nodo inicial y

su
nodo final.
Por definición, los grafos dirigidos no contienen
bucles.
Un
grafo mixto es aquel que se define con la capacidad de
poder contener aristas dirigidas y no dirigidas. Tanto los grafos
dirigidos como los no dirigidos son casos particulares de este.
Variantes sobre las definiciones principales
Algunas aplicaciones requieren extensiones más generales a las dos
propuestas clásicas de grafos. Aunque la definición original los
permite, según la aplicación concreta pueden ser válidos o no. A veces

o

pueden ser un multiconjunto, pudiendo haber más de una arista entre cada par de vértices. La palabra
grafo
(a secas) puede permitir o no múltiples aristas entre cada par de
vértices, dependiendo del autor de la referencia consultada. Si se
quiere remarcar la inexistencia de múltiples aristas entre cada par de
vértices (y en el caso no dirigido, excluir bucles) el grafo puede
llamarse
simple. Por otra parte, si se quiere asegurar la posibilidad de permitir múltiples aristas, el grafo puede llamarse
multigrafo (a veces se utiliza el término
pseudografo para indicar que se permiten tanto bucles como múltiples aristas entre cada par de vértices).
Propiedades
- Adyacencia: dos aristas son adyacentes si tienen un vértice en común, y dos vértices son adyacentes si una arista los une.
- Incidencia: una arista es incidente a un vértice si ésta lo une a otro.
- Ponderación: corresponde a una función que a cada arista le
asocia un valor (costo, peso, longitud, etc.), para aumentar la
expresividad del modelo. Esto se usa mucho para problemas de
optimización, como el del vendedor viajero o del camino más corto.
- Etiquetado: distinción que se hace a los vértices y/o aristas mediante una marca que los hace unívocamente distinguibles del resto.
Ejemplos
La imagen es una representación del siguiente grafo:
- V:={1,2,3,4,5,6}
- E:={{1,2},{1,5},{2,3},{2,5},{3,4},{4,5},{4,6}}
El hecho que el vértice 1 sea adyacente con el vértice 2 puede ser denotado como 1 ~ 2.
- En la teoría de las categorías una categoría puede ser considerada como un multigrafo dirigido, con los objetos como vértices y los morfismos como aristas dirigidas.
- En ciencias de la computación los grafos dirigidos son usados para
representar máquinas de estado finito y algunas otras estructuras
discretas.
- Una relación binaria R en un conjunto X es un grafo dirigido simple. Dos vértices a, b en X están conectados por una arista dirigida ab si aRb.
Grafos particulares
Existen grafos que poseen propiedades destacables. Algunos ejemplos básicos son:
- Grafo nulo:
aquel que no tiene vértices ni aristas. Nótese que algunas personas
exigen que el conjunto de vértices no sea vacío en la definición de
grafo.
- Grafo vacío: aquel que no tiene aristas.
- Grafo trivial: aquel que tiene un vértice y ninguna arista.
- Grafo simple: aquel que no posee bucles ni aristas paralelas. Consultar variantes en esta definición.
- Multigrafo (o pseudografo): G es multigrafo si y solo si no es simple. Consultar variantes en esta definición.
- Grafo completo: grafo simple en el que cada par de vértices están
unidos por una arista, es decir, contiene todas las posibles aristas.
- Grafo bipartito: sea
 una partición del conjunto de vértices
una partición del conjunto de vértices  , es aquel donde cada arista tiene un vértice en
, es aquel donde cada arista tiene un vértice en  y otro en
y otro en  .
.
- Grafo bipartito completo: sea
 una partición del conjunto de vértices
una partición del conjunto de vértices  , es aquel donde cada vértice en
, es aquel donde cada vértice en  es adyacente sólo a cada vértice en
es adyacente sólo a cada vértice en  , y viceversa.
, y viceversa.
- Grafo plano: aquel que puede ser dibujado en el plano cartesiano sin cruce de aristas.
- Árbol: grafo conexo sin ciclos.
- Grafo rueda: grafo con n vértices que se forma conectando un único vértice a todos los vértices de un ciclo-(n-1).
- Grafo perfecto aquel que el número cromático de cada subgrafo inducido es igual al tamaño del mayor clique de ese subgrafo.
Una generalización de los grafos son los llamados hipergrafos
Ciclo hamiltoniano
Un
camino hamiltoniano,
en el campo matemático de la teoría de grafos, es un camino de un
grafo, una sucesión de aristas adyacentes, que visita todos los vértices
del grafo una sola vez. Si además el último vértice visitado es
adyacente al primero, el camino es un
ciclo hamiltoniano.
El problema de encontrar un ciclo (o camino) hamiltoniano en un grafo arbitrario se sabe que es NP-completo.
Los
caminos y ciclos hamiltonianos se llaman así en honor de William Rowan
Hamilton, inventor de un juego que consistía en encontrar un ciclo
hamiltoniano en las aristas de un grafo de un dodecaedro. Hamilton
resolvió este problema usando cuaterniones, aunque su solución no era
generalizable a todos los grafos.
Definición
Un camino hamiltoniano es un camino que pasa por cada vértice
exactamente una vez. Un grafo que contiene un camino hamiltoniano se
denomina un ciclo hamiltoniano si es un ciclo
que pasa por cada vértice exactamente una vez (excepto el vértice del
que parte y al cual llega). Un grafo que contiene un ciclo hamiltoniano
se dice grafo hamiltoniano.
Estos conceptos se pueden extender para los grafos dirigidos los cuales son igual a un carro.
Ejemplos
- Todos los grafos ciclos son hamiltonianos.
- Todos los sólidos platónicos, (tetraedro, el cubo, el octaedro, el
dodecaedro y el icosaedro.) considerados como grafos, son hamiltonianos.1
Notas
Cualquier ciclo hamiltoniano puede ser convertido en un camino
hamiltoniano si se elimina cualquiera de sus aristas, pero un camino
hamiltoniano puede ser extendido en ciclo sólo si los vértices de los
extremos son adyacentes.
Teorema de Bondy-Chvátal
La
mejor caracterización de los grafos hamiltonianos fue dada en 1972 por
el teorema de Bondy-Chvátal que generalizaba los resultados
anteriormente encontrados por G. A. Dirac. Básicamente dice que un grafo
es hamiltoniano si
existen suficientes aristas. Primero debemos definir lo que es la
cerradura de un grafo.
Dado un grafo
G con
n vértices, la
cerradura (cl(
G)) es construida de manera única a partir de
G agregando toda arista u-v si el par
no adyacente de vértices
u y
v cumple que grado(v) + grado(u) ≥ n
Un grafo es hamiltoniano si y sólo si su grafo cerradura es hamiltoniano.
Bondy-Chvátal (1972)
|
Como todos los grafos completos son hamiltonianos, todos los grafos
cuya cerradura sea completa son hamiltonianos. Este resultado se basa en
los teoremas de Dirac y Ore.
Un grafo con n vértices (n > 3) es hamiltoniano si cada vértice tiene grado mayor o igual a n/2.
Dirac (1952)
|
Un grafo con n vértices (n > 3) es hamiltoniano si la suma de los grados de 2 vértices no adyacentes es mayor o igual que n.
Ore (1960)
|
Sin embargo, existe un resultado anterior a todos estos teoremas.
Un grafo con n vértices (n ≥ 2) es hamiltoniano si la suma de los grados de 2 vértices es mayor o igual que n-1.
L.Redei (1934)
|
Como puede verse, este teorema pide más hipótesis que los anteriores ya que la propiedad de los grados debe cumplirse
para todo vértice en el grafo.
Ciclo euleriano
En la teoría de grafos, un camino euleriano
es un camino que pasa por cada arista una y solo una vez. Un ciclo o
circuito euleriano es un camino cerrado que recorre cada arista
exactamente una vez. El problema de encontrar dichos caminos fue
discutido por primera vez por Leonhard Euler, en el famoso problema de los puentes de Königsberg.
Ciclos eulerianos
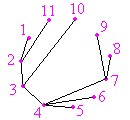
Dibujar un sobre abierto, como el de la imagen, sin levantar el lápiz
del papel ni pasar dos veces por el mismo sitio, es posible. En cambio,
dibujar el sobre cerrado (prescindiendo del punto 5 y sus líneas
adyacentes) es imposible.
En la imagen,

es un ciclo euleriano, luego es un grafo euleriano.
Un grafo es una representación, un modelo, compuesto por un número
determinado de vértices (nodos) y un número de arcos (aristas) que los
relacionan, cada arista o arco tiene la capacidad de relacionar dos
nodos. La palabra ciclo se emplea en teoría de grafos para indicar un
camino cerrado
en un grafo, es decir, en que el nodo de inicio y el nodo final son el
mismo, como contrapartida un camino hamiltoniano es un camino que
recorre todos los vértices de un grafo sin pasar dos veces por el mismo
vértice. Si el camino es cerrado se dice un ciclo hamiltoniano.
Si un grafo admite un ciclo euleriano, se denomina
grafo euleriano.
Historia
Artículo principal: Problema de los puentes de Königsberg
El
origen de la teoría de los ciclos eulerianos fue planteado y resuelto
por el propio Leonhard Euler en 1736 en un problema que tiene el nombre
de
Siete puentes de la ciudad de Königsberg (Prusia oriental en el siglo XVIII y actualmente, Kaliningrado, provincia rusa) dando origen a la Teoría de los grafos.
El problema se enuncia de la siguiente forma: Dos islas en el río Pregel,
en Königsberg se unen entre ellas y con la tierra firme mediante siete
puentes. ¿Es posible dar un paseo empezando por una cualquiera de las
cuatro partes de tierra firme, cruzando cada puente una sola vez y
volviendo al punto de partida?

Euler enfocó el problema representando cada parte de tierra por un
punto y cada puente, por una línea, uniendo los puntos que se
corresponden. Entonces, el problema anterior se puede trasladar a la
siguiente pregunta: ¿se puede recorrer el dibujo sin repetir las líneas?

Euler demostró que no era posible puesto que el número de líneas que
inciden en cada punto no es par (condición necesaria para entrar y salir
de cada punto, y para regresar al punto de partida, por caminos
distintos en todo momento).
Casos
Dado un grafo conexo (no existen nodos aislados) y no dirigido

, si

tiene exactamente dos vértices de grado impar, entonces

tiene un camino euleriano no cerrado. En caso de que todos los vértices tengan grado par,

tiene un ciclo euleriano.
Teorema
Dado

no orientado y conexo; si tiene

nodos de grado impar, entonces

puede ser escrito como unión de

caminos (simples) distintos sobre los arcos y valen las siguientes expresiones:
-
- 1)
 es euleriano;
es euleriano; - 2)
 con grado
con grado  y par.
y par. - 3)
 todos disjuntos (caminos distintos) en los arcos,
todos disjuntos (caminos distintos) en los arcos, - es decir
 con
con 

va de un nodo de grado impar a un nodo de grado impar.
Un grafo admite un camino euleriano cuando tiene exactamente
dos nodos de grado impar (conexos a los caminos).
Propiedades
- Un grafo conexo y no dirigido se dice que es euleriano si cada vértice tiene un grado par.
- Un grafo no dirigido es euleriano si es conexo y si se puede descomponer en uno con los vértices disjuntos.
- Si un grafo no dirigido G es euleriano entonces su gráfo-línea L(G) se dice que es también euleriano.
- Un grafo dirigido es euleriano si es conexo y cada vértice tiene grados internos iguales a los externos.
- Un grafo no dirigido se dice que es susceptible de ser recorrido (en inglés: traversable) si es conexo y dos vértices en el grafo tienen grado impar.
Contando circuitos eulerianos en dígrafos
El número de circuitos euleriano en los dígrafos puede ser calculado mediante el teorema denominado en Inglés:
BEST-theorem, procedente de los nombres de sus fundadores: de
Bruijn, van Aardenne-
Ehrenfest,
Smith y
Tutte.
En dicho teorema se menciona que dado un dígrafo euleriano
G := (
V,
E), el número ciclos eulerianos no-equivalentes en el grafo es

o equivalentemente

siendo
C cualquier cofactor de la matriz laplaciana de
G.
Representación de grafos
Existen diferentes formas de representar un grafo (simple), además de
la geométrica y muchos métodos para almacenarlos en una computadora. La
estructura de datos usada depende de las características del grafo y el algoritmo
usado para manipularlo. Entre las estructuras más sencillas y usadas se
encuentran las listas y las matrices, aunque frecuentemente se usa una
combinación de ambas. Las listas son preferidas en grafos dispersos
porque tienen un eficiente uso de la memoria. Por otro lado, las
matrices proveen acceso rápido, pero pueden consumir grandes cantidades
de memoria.
Estructura de lista
- lista de incidencia - Las aristas son representadas con un
vector de pares (ordenados, si el grafo es dirigido), donde cada par
representa una de las aristas,.
- lista de adyacencia
- Cada vértice tiene una lista de vértices los cuales son adyacentes a
él. Esto causa redundancia en un grafo no dirigido (ya que A existe en
la lista de adyacencia de B y viceversa), pero las búsquedas son más
rápidas, al costo de almacenamiento extra.
- lista de grados - También llamada secuencia de grados o sucesión gráfica de un grafo no-dirigido es una secuencia de números, que corresponde a los grados de los vértices del grafo.
Estructuras matriciales
- Matriz de adyacencia - El grafo está representado por una matriz cuadrada M de tamaño
 , donde
, donde  es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento
es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento  es 1, de lo contrario, es 0.
es 1, de lo contrario, es 0.
- Matriz de incidencia - El grafo está representado por una
matriz de A (aristas) por V (vértices), donde [vértice, arista] contiene
la información de la arista (1 - conectado, 0 - no conectado)
| Grafo G(V,A) |
Conjuntos |
Matriz de adyacencia |
Matriz de incidencia |
Secuencia de grados |
Lista de Adyacencia |
 |
V = { 1, 2, 3, 4, 5, 6 }
A = { {1,1}, {1,2}, {1,5},
{2,3}, {2,5}, {3,4},
{4,5}, {4,6} } |
 |
 |
(4,3,3,3,2,1) |
{ {1,2,5}, {3,5}, {4}, {5,6} } |
Problemas de teoría de grafos
Ciclos y caminos hamiltonianos
Ejemplo de un ciclo Hamiltoniano.
Un
ciclo es una sucesión de aristas adyacentes, donde no se recorre dos veces la misma arista, y donde se regresa al punto inicial. Un
ciclo hamiltoniano tiene además que recorrer todos los vértices exactamente una vez (excepto el vértice del que parte y al cual llega).
Por ejemplo, en un museo grande (al estilo del Louvre),
lo idóneo sería recorrer todas las salas una sola vez, esto es buscar
un ciclo hamiltoniano en el grafo que representa el museo (los vértices
son las salas, y las aristas los corredores o puertas entre ellas).
Se habla también de Camino hamiltoniano
si no se impone regresar al punto de partida, como en un museo con una
única puerta de entrada. Por ejemplo, un caballo puede recorrer todas
las casillas de un tablero de ajedrez sin pasar dos veces por la misma:
es un camino hamiltoniano. Ejemplo de un ciclo hamiltoniano en el grafo
del dodecaedro.
Hoy en día, no se conocen métodos generales para hallar un ciclo hamiltoniano en tiempo polinómico,
siendo la búsqueda por fuerza bruta de todos los posibles caminos u
otros métodos excesivamente costosos. Existen, sin embargo, métodos para
descartar la existencia de ciclos o caminos hamiltonianos en grafos
pequeños.
El problema de determinar la existencia de ciclos hamiltonianos, entra en el conjunto de los NP-completos.
Un grafo es plano si se puede dibujar sin cruces de aristas. El problema de las tres casas y los tres pozos tiene solución sobre el toro, pero no en el plano.
Grafos planos
Cuando un grafo o multigrafo se puede dibujar en un plano sin que dos segmentos se corten, se dice que es plano.
Un juego muy conocido es el siguiente: Se dibujan tres casas y tres
pozos. Todos los vecinos de las casas tienen el derecho de utilizar los
tres pozos. Como no se llevan bien en absoluto, no quieren cruzarse
jamás. ¿Es posible trazar los nueve caminos que juntan las tres casas
con los tres pozos sin que haya cruces?
Cualquier disposición de las casas, los pozos y los caminos implica la presencia de al menos un cruce.
Sea K
n el grafo completo con
n vértices, K
n, p es el grafo bipartito de
n y
p vértices.
El juego anterior equivale a descubrir si el grafo bipartito completo K
3,3 es
plano,
es decir, si se puede dibujar en un plano sin que haya cruces, siendo
la respuesta que no. En general, puede determinarse que un grafo
no es plano, si en su diseño puede encontrase una estructura análoga (conocida como
menor) a K
5 o a K
3,3.
Establecer qué grafos son planos no es obvio, y es un problema que tiene que ver con topología.
Coloración de grafos
Si G=(V, E) es un grafo no dirigido, una coloración propia de G,
ocurre cuando coloreamos los vértices de G de modo que si {a, b} es una
arista en G entonces a y b tienen diferentes colores. (Por lo tanto, los
vértices adyacentes tienen colores diferentes). El número mínimo de
colores necesarios para una coloración propia de G es el número
cromático de G y se escribe como C (G). Sea G un grafo no dirigido sea λ
el número de colores disponibles para la coloración propia de los
vértices de G. Nuestro objetivo es encontrar una función polinomial P
(G,λ), en la variable λ, llamada
polinomio cromático de G, que nos indique el número de coloraciones propias diferentes de los vértices de G, usando un máximo de λ colores.
Descomposición de polinomios cromáticos. Si G=(V, E) es un grafo
conexo y e pertenece a Ε, entonces: P (G,λ)=P (G+e,λ)+P (G/e,λ), donde
G/e es el grafo se obtene por contracción de aristas.
Para cualquier grafo G, el término constante en P (G,λ) es 0
Sea G=(V, E) con |E|>0 entonces, la suma de los coeficientes de P (G,λ) es 0.
Sea G=(V, E), con
a,
b pertenecientes al conjunto de vértices
V
pero {a, b}=e, no perteneciente a al conjunto de aristas E. Escribimos
G+e para el grafo que se obtiene de G al añadir la arista e={a, b}. Al
identificar los vértices a y b en G, obtenemos el subgrafo G++e de
G.0000
Teorema de los cuatro colores
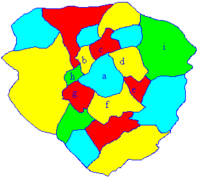
Mapa coloreado con 4-colores.
Grafo dual asociado al mapa con una 4-vértice coloración.
Otro problema famoso relativo a los grafos: ¿Cuántos colores son
necesarios para dibujar un mapa político, con la condición obvia que dos
países adyacentes no puedan tener el mismo color? Se supone que los
países son de un solo pedazo, y que el mundo es esférico o plano. En un
mundo en forma de toroide; el teorema siguiente no es válido:
Cuatro colores son siempre suficientes para colorear un mapa.
El mapa siguiente muestra que tres colores no bastan: Si se empieza por el país central
a y se esfuerza uno en utilizar el menor número de colores, entonces en la corona alrededor de
a alternan dos colores. Llegando al país
h se tiene que introducir un cuarto color. Lo mismo sucede en
i si se emplea el mismo método.
La forma precisa de cada país no importa; lo único relevante es saber
qué país toca a qué otro. Estos datos están incluidos en el grafo donde
los vértices son los países y las aristas conectan los que justamente
son adyacentes. Entonces la cuestión equivale a atribuir a cada vértice
un color distinto del de sus vecinos.
Hemos visto que tres colores no son suficientes, y demostrar que con
cinco siempre se llega, es bastante fácil. Pero el teorema de los cuatro
colores no es nada obvio. Prueba de ello es que se han tenido que
emplear ordenadores para acabar la demostración (se ha hecho un programa
que permitió verificar una multitud de casos, lo que ahorró muchísimo
tiempo a los matemáticos). Fue la primera vez que la comunidad
matemática aceptó una demostración asistida por ordenador, lo que creó
en su día una cierta polémica dentro de dicha comunidad.
Caracterización de grafos
Grafos simples
Un grafo es
simple si a lo sumo existe una arista uniendo dos
vértices cualesquiera. Esto es equivalente a decir que una arista
cualquiera es la única que une dos vértices específicos.
Un grafo que no es simple se denomina multigrafo.
Grafos conexos
Un grafo es conexo si cada par de vértices está conectado por un
camino; es decir, si para cualquier par de vértices (a, b), existe al
menos un camino posible desde
a hacia
b.
Un grafo es doblemente conexo si cada par de vértices está conectado
por al menos dos caminos disjuntos; es decir, es conexo y no existe un
vértice tal que al sacarlo el grafo resultante sea disconexo.
Es posible determinar si un grafo es conexo usando un algoritmo Búsqueda en anchura (BFS) o Búsqueda en profundidad (DFS).
En
términos matemáticos la propiedad de un grafo de ser (fuertemente)
conexo permite establecer con base en él una relación de equivalencia
para sus vértices, la cual lleva a una partición de éstos en
"componentes (fuertemente) conexas", es decir, porciones del grafo, que
son (fuertemente) conexas cuando se consideran como grafos aislados.
Esta propiedad es importante para muchas demostraciones en teoría de
grafos.
Grafos completos
Un grafo es
completo si existen aristas uniendo
todos los pares posibles de vértices. Es decir, todo par de vértices (a, b) debe tener una arista
e que los une.
El conjunto de los grafos completos es denominado usualmente

, siendo

el grafo completo de
n vértices.
Un

, es decir, grafo completo de

vértices tiene exactamente
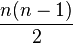
aristas.
La representación gráfica de los

como los vértices de un polígono regular da cuenta de su peculiar estructura.
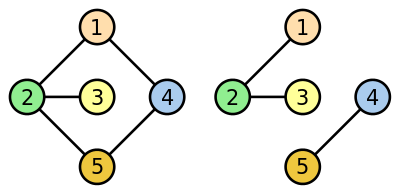
Grafos bipartitos
Un grafo G es bipartito si puede expresar como

(es decir, sus vértices son la unión de dos grupos de vértices), bajo las siguientes condiciones:
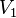 y
y 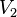 son disjuntos y no vacíos.
son disjuntos y no vacíos.- Cada arista de A une un vértice de V1 con uno de V2.
- No existen aristas uniendo dos elementos de V1; análogamente para V2.
Bajo estas condiciones, el grafo se considera bipartito, y puede
describirse informalmente como el grafo que une o relaciona dos
conjuntos de elementos diferentes, como aquellos resultantes de los
ejercicios y puzzles en los que debe unirse un elemento de la columna A
con un elemento de la columna B.
Homeomorfismo de grafos
Dos grafos

y
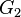
son homeomorfos si ambos pueden obtenerse a partir del mismo grafo con una sucesión de subdivisiones elementales de aristas.
Árboles
Un grafo que no tiene ciclos y que conecta a todos los puntos, se llama un
árbol. En un grafo con
n vértices, los árboles tienen exactamente
n - 1 aristas, y hay
nn-2
árboles posibles. Su importancia radica en que los árboles son grafos
que conectan todos los vértices utilizando el menor número posible de
aristas. Un importante campo de aplicación de su estudio se encuentra en
el análisis filogenético,
el de la filiación de entidades que derivan unas de otras en un proceso
evolutivo, que se aplica sobre todo a la averiguación del parentesco
entre especies; aunque se ha usado también, por ejemplo, en el estudio
del parentesco entre lenguas.
Grafos ponderados o etiquetados
En muchos casos, es preciso atribuir a cada arista un número específico, llamado
valuación,
ponderación o
coste según el contexto, y se obtiene así un
grafo valuado.
Formalmente, es un grafo con una función v: A →
R+.
Por ejemplo, un representante comercial tiene que visitar
n
ciudades conectadas entre sí por carreteras; su interés previsible será
minimizar la distancia recorrida (o el tiempo, si se pueden prever
atascos). El grafo correspondiente tendrá como vértices las ciudades,
como aristas las carreteras y la valuación será la distancia entre
ellas.
Y, de momento, no se conocen métodos generales para hallar un ciclo de valuación mínima, pero sí para los caminos desde
a hasta
b, sin más condición.
Diámetro
En la figura se nota que K4 es plano (desviando la arista ab al exterior del cuadrado), que K5 no lo es, y que K3,2 lo es también (desvíos en gris).
En un grafo, la distancia entre dos vértices es el menor número de aristas de un recorrido entre ellos. El
diámetro, en una figura como en un grafo, es la mayor distancia de entre todos los pares de puntos de la misma.
El diámetro de los K
n es 1, y el de los K
n,
p es 2. Un diámetro infinito puede significar que el grafo tiene una infinidad de vértices o simplemente que no es
conexo. También se puede considerar el
diámetro promedio, como el promedio de las distancias entre dos vértices.
El mundo de Internet ha puesto de moda esa idea del diámetro: Si
descartamos los sitios que no tienen enlaces, y escogemos dos páginas
web al azar: ¿En cuántos
clics
se puede pasar de la primera a la segunda? El resultado es el diámetro
de la Red, vista como un grafo cuyos vértices son los sitios, y cuyas
aristas son lógicamente los enlaces.
En el mundo real hay una analogía: tomando al azar dos seres humanos
del mundo, ¿En cuántos saltos se puede pasar de uno a otro, con la
condición de sólo saltar de una persona a otra cuando ellas se conocen
personalmente? Con esta definición, se estima que el diámetro de la
humanidad es de... ¡ocho solamente!
Este concepto refleja mejor la complejidad de una red que el número de sus elementos.
 no es un menor de G.
no es un menor de G.




 es un par ordenado
es un par ordenado  , donde:
, donde: es un conjunto de vértices o nodos, y
es un conjunto de vértices o nodos, y es un conjunto de aristas o arcos, que relacionan estos nodos.
es un conjunto de aristas o arcos, que relacionan estos nodos. .
. es igual al número de arcos que lo tienen como extremo.
es igual al número de arcos que lo tienen como extremo.
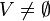
 es un conjunto de pares no ordenados de elementos de
es un conjunto de pares no ordenados de elementos de  .
. , de manera que
, de manera que  . Para los grafos, estos conjuntos pertenecen al conjunto potencia de
. Para los grafos, estos conjuntos pertenecen al conjunto potencia de 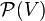 , y son de cardinalidad 2.
, y son de cardinalidad 2.
 es un conjunto de pares ordenados de elementos de
es un conjunto de pares ordenados de elementos de  ,
,  es su nodo inicial y
es su nodo inicial y  su nodo final.
su nodo final. una partición del conjunto de vértices
una partición del conjunto de vértices  y otro en
y otro en  .
.

 es un ciclo euleriano, luego es un grafo euleriano.
es un ciclo euleriano, luego es un grafo euleriano.

 , si
, si  tiene exactamente dos vértices de grado impar, entonces
tiene exactamente dos vértices de grado impar, entonces  no orientado y conexo; si tiene
no orientado y conexo; si tiene  nodos de grado impar, entonces
nodos de grado impar, entonces  caminos (simples) distintos sobre los arcos y valen las siguientes expresiones:
caminos (simples) distintos sobre los arcos y valen las siguientes expresiones: con grado
con grado  y par.
y par. todos disjuntos (caminos distintos) en los arcos,
todos disjuntos (caminos distintos) en los arcos, con
con 
 va de un nodo de grado impar a un nodo de grado impar.
va de un nodo de grado impar a un nodo de grado impar.

 , donde
, donde  es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento
es el número de vértices. Si hay una arista entre un vértice x y un vértice y, entonces el elemento  es 1, de lo contrario, es 0.
es 1, de lo contrario, es 0.





 , siendo
, siendo  el grafo completo de n vértices.
el grafo completo de n vértices.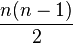 aristas.
aristas. (es decir, sus vértices son la unión de dos grupos de vértices), bajo las siguientes condiciones:
(es decir, sus vértices son la unión de dos grupos de vértices), bajo las siguientes condiciones: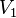 y
y 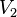 son disjuntos y no vacíos.
son disjuntos y no vacíos. y
y 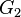 son homeomorfos si ambos pueden obtenerse a partir del mismo grafo con una sucesión de subdivisiones elementales de aristas.
son homeomorfos si ambos pueden obtenerse a partir del mismo grafo con una sucesión de subdivisiones elementales de aristas.